Amortization Calculator
| Enter Loan Data |
|---|
| Loan Amount | |
| Annual Interest Rate | |
| Loan Duration | |
| Start Date | |
| Extra Payments |
| Monthly from | ||
| Yearly from | ||
To deliver an estimate...
...press "Calculate" button
The loan will be paid off in 120 month(s) without extra payments. |
| Total of 120 Payments | $260,463.07 |
| Monthly Payment | $2,170.53 |
| Total Interest | $60,463.07 |
| Loan Distribution |
|---|
| Loan Balance, Interest Payments |
|---|
Monthly amortization schedule ↑
| Month | Opening balance | Interest | Principal | Ending balance |
|---|---|---|---|---|
| Jul 2025 | $200,000.00 | $916.67 | $1,253.86 | $198,746.14 |
| Aug 2025 | $198,746.14 | $910.92 | $1,259.61 | $197,486.54 |
| Sep 2025 | $197,486.54 | $905.15 | $1,265.38 | $196,221.16 |
| Oct 2025 | $196,221.16 | $899.35 | $1,271.18 | $194,949.98 |
| Nov 2025 | $194,949.98 | $893.52 | $1,277.00 | $193,672.97 |
| Dec 2025 | $193,672.97 | $887.67 | $1,282.86 | $192,390.12 |
| Jan 2026 | $192,390.12 | $881.79 | $1,288.74 | $191,101.38 |
| Feb 2026 | $191,101.38 | $875.88 | $1,294.64 | $189,806.73 |
| Mar 2026 | $189,806.73 | $869.95 | $1,300.58 | $188,506.16 |
| Apr 2026 | $188,506.16 | $863.99 | $1,306.54 | $187,199.62 |
| May 2026 | $187,199.62 | $858.00 | $1,312.53 | $185,887.09 |
| Jun 2026 | $185,887.09 | $851.98 | $1,318.54 | $184,568.55 |
| End of year 1 | ||||
| Jul 2026 | $184,568.55 | $845.94 | $1,324.59 | $183,243.96 |
| Aug 2026 | $183,243.96 | $839.87 | $1,330.66 | $181,913.30 |
| Sep 2026 | $181,913.30 | $833.77 | $1,336.76 | $180,576.55 |
| Oct 2026 | $180,576.55 | $827.64 | $1,342.88 | $179,233.66 |
| Nov 2026 | $179,233.66 | $821.49 | $1,349.04 | $177,884.62 |
| Dec 2026 | $177,884.62 | $815.30 | $1,355.22 | $176,529.40 |
| Jan 2027 | $176,529.40 | $809.09 | $1,361.43 | $175,167.97 |
| Feb 2027 | $175,167.97 | $802.85 | $1,367.67 | $173,800.30 |
| Mar 2027 | $173,800.30 | $796.58 | $1,373.94 | $172,426.36 |
| Apr 2027 | $172,426.36 | $790.29 | $1,380.24 | $171,046.12 |
| May 2027 | $171,046.12 | $783.96 | $1,386.56 | $169,659.56 |
| Jun 2027 | $169,659.56 | $777.61 | $1,392.92 | $168,266.64 |
| End of year 2 | ||||
| Jul 2027 | $168,266.64 | $771.22 | $1,399.30 | $166,867.33 |
| Aug 2027 | $166,867.33 | $764.81 | $1,405.72 | $165,461.62 |
| Sep 2027 | $165,461.62 | $758.37 | $1,412.16 | $164,049.46 |
| Oct 2027 | $164,049.46 | $751.89 | $1,418.63 | $162,630.82 |
| Nov 2027 | $162,630.82 | $745.39 | $1,425.13 | $161,205.69 |
| Dec 2027 | $161,205.69 | $738.86 | $1,431.67 | $159,774.02 |
| Jan 2028 | $159,774.02 | $732.30 | $1,438.23 | $158,335.80 |
| Feb 2028 | $158,335.80 | $725.71 | $1,444.82 | $156,890.98 |
| Mar 2028 | $156,890.98 | $719.08 | $1,451.44 | $155,439.53 |
| Apr 2028 | $155,439.53 | $712.43 | $1,458.09 | $153,981.44 |
| May 2028 | $153,981.44 | $705.75 | $1,464.78 | $152,516.66 |
| Jun 2028 | $152,516.66 | $699.03 | $1,471.49 | $151,045.17 |
| End of year 3 | ||||
| Jul 2028 | $151,045.17 | $692.29 | $1,478.24 | $149,566.94 |
| Aug 2028 | $149,566.94 | $685.52 | $1,485.01 | $148,081.93 |
| Sep 2028 | $148,081.93 | $678.71 | $1,491.82 | $146,590.11 |
| Oct 2028 | $146,590.11 | $671.87 | $1,498.65 | $145,091.46 |
| Nov 2028 | $145,091.46 | $665.00 | $1,505.52 | $143,585.93 |
| Dec 2028 | $143,585.93 | $658.10 | $1,512.42 | $142,073.51 |
| Jan 2029 | $142,073.51 | $651.17 | $1,519.36 | $140,554.15 |
| Feb 2029 | $140,554.15 | $644.21 | $1,526.32 | $139,027.83 |
| Mar 2029 | $139,027.83 | $637.21 | $1,533.31 | $137,494.52 |
| Apr 2029 | $137,494.52 | $630.18 | $1,540.34 | $135,954.18 |
| May 2029 | $135,954.18 | $623.12 | $1,547.40 | $134,406.78 |
| Jun 2029 | $134,406.78 | $616.03 | $1,554.49 | $132,852.28 |
| End of year 4 | ||||
| Jul 2029 | $132,852.28 | $608.91 | $1,561.62 | $131,290.66 |
| Aug 2029 | $131,290.66 | $601.75 | $1,568.78 | $129,721.88 |
| Sep 2029 | $129,721.88 | $594.56 | $1,575.97 | $128,145.92 |
| Oct 2029 | $128,145.92 | $587.34 | $1,583.19 | $126,562.73 |
| Nov 2029 | $126,562.73 | $580.08 | $1,590.45 | $124,972.28 |
| Dec 2029 | $124,972.28 | $572.79 | $1,597.74 | $123,374.55 |
| Jan 2030 | $123,374.55 | $565.47 | $1,605.06 | $121,769.49 |
| Feb 2030 | $121,769.49 | $558.11 | $1,612.42 | $120,157.07 |
| Mar 2030 | $120,157.07 | $550.72 | $1,619.81 | $118,537.27 |
| Apr 2030 | $118,537.27 | $543.30 | $1,627.23 | $116,910.04 |
| May 2030 | $116,910.04 | $535.84 | $1,634.69 | $115,275.35 |
| Jun 2030 | $115,275.35 | $528.35 | $1,642.18 | $113,633.17 |
| End of year 5 | ||||
| Jul 2030 | $113,633.17 | $520.82 | $1,649.71 | $111,983.46 |
| Aug 2030 | $111,983.46 | $513.26 | $1,657.27 | $110,326.19 |
| Sep 2030 | $110,326.19 | $505.66 | $1,664.86 | $108,661.33 |
| Oct 2030 | $108,661.33 | $498.03 | $1,672.49 | $106,988.83 |
| Nov 2030 | $106,988.83 | $490.37 | $1,680.16 | $105,308.67 |
| Dec 2030 | $105,308.67 | $482.66 | $1,687.86 | $103,620.81 |
| Jan 2031 | $103,620.81 | $474.93 | $1,695.60 | $101,925.22 |
| Feb 2031 | $101,925.22 | $467.16 | $1,703.37 | $100,221.85 |
| Mar 2031 | $100,221.85 | $459.35 | $1,711.18 | $98,510.67 |
| Apr 2031 | $98,510.67 | $451.51 | $1,719.02 | $96,791.65 |
| May 2031 | $96,791.65 | $443.63 | $1,726.90 | $95,064.76 |
| Jun 2031 | $95,064.76 | $435.71 | $1,734.81 | $93,329.95 |
| End of year 6 | ||||
| Jul 2031 | $93,329.95 | $427.76 | $1,742.76 | $91,587.18 |
| Aug 2031 | $91,587.18 | $419.77 | $1,750.75 | $89,836.43 |
| Sep 2031 | $89,836.43 | $411.75 | $1,758.78 | $88,077.66 |
| Oct 2031 | $88,077.66 | $403.69 | $1,766.84 | $86,310.82 |
| Nov 2031 | $86,310.82 | $395.59 | $1,774.93 | $84,535.89 |
| Dec 2031 | $84,535.89 | $387.46 | $1,783.07 | $82,752.82 |
| Jan 2032 | $82,752.82 | $379.28 | $1,791.24 | $80,961.57 |
| Feb 2032 | $80,961.57 | $371.07 | $1,799.45 | $79,162.12 |
| Mar 2032 | $79,162.12 | $362.83 | $1,807.70 | $77,354.42 |
| Apr 2032 | $77,354.42 | $354.54 | $1,815.98 | $75,538.44 |
| May 2032 | $75,538.44 | $346.22 | $1,824.31 | $73,714.13 |
| Jun 2032 | $73,714.13 | $337.86 | $1,832.67 | $71,881.46 |
| End of year 7 | ||||
| Jul 2032 | $71,881.46 | $329.46 | $1,841.07 | $70,040.39 |
| Aug 2032 | $70,040.39 | $321.02 | $1,849.51 | $68,190.89 |
| Sep 2032 | $68,190.89 | $312.54 | $1,857.98 | $66,332.90 |
| Oct 2032 | $66,332.90 | $304.03 | $1,866.50 | $64,466.40 |
| Nov 2032 | $64,466.40 | $295.47 | $1,875.05 | $62,591.35 |
| Dec 2032 | $62,591.35 | $286.88 | $1,883.65 | $60,707.70 |
| Jan 2033 | $60,707.70 | $278.24 | $1,892.28 | $58,815.42 |
| Feb 2033 | $58,815.42 | $269.57 | $1,900.95 | $56,914.46 |
| Mar 2033 | $56,914.46 | $260.86 | $1,909.67 | $55,004.79 |
| Apr 2033 | $55,004.79 | $252.11 | $1,918.42 | $53,086.37 |
| May 2033 | $53,086.37 | $243.31 | $1,927.21 | $51,159.16 |
| Jun 2033 | $51,159.16 | $234.48 | $1,936.05 | $49,223.12 |
| End of year 8 | ||||
| Jul 2033 | $49,223.12 | $225.61 | $1,944.92 | $47,278.20 |
| Aug 2033 | $47,278.20 | $216.69 | $1,953.83 | $45,324.36 |
| Sep 2033 | $45,324.36 | $207.74 | $1,962.79 | $43,361.57 |
| Oct 2033 | $43,361.57 | $198.74 | $1,971.79 | $41,389.79 |
| Nov 2033 | $41,389.79 | $189.70 | $1,980.82 | $39,408.97 |
| Dec 2033 | $39,408.97 | $180.62 | $1,989.90 | $37,419.06 |
| Jan 2034 | $37,419.06 | $171.50 | $1,999.02 | $35,420.04 |
| Feb 2034 | $35,420.04 | $162.34 | $2,008.18 | $33,411.86 |
| Mar 2034 | $33,411.86 | $153.14 | $2,017.39 | $31,394.47 |
| Apr 2034 | $31,394.47 | $143.89 | $2,026.63 | $29,367.84 |
| May 2034 | $29,367.84 | $134.60 | $2,035.92 | $27,331.91 |
| Jun 2034 | $27,331.91 | $125.27 | $2,045.25 | $25,286.66 |
| End of year 9 | ||||
| Jul 2034 | $25,286.66 | $115.90 | $2,054.63 | $23,232.03 |
| Aug 2034 | $23,232.03 | $106.48 | $2,064.05 | $21,167.99 |
| Sep 2034 | $21,167.99 | $97.02 | $2,073.51 | $19,094.48 |
| Oct 2034 | $19,094.48 | $87.52 | $2,083.01 | $17,011.47 |
| Nov 2034 | $17,011.47 | $77.97 | $2,092.56 | $14,918.91 |
| Dec 2034 | $14,918.91 | $68.38 | $2,102.15 | $12,816.77 |
| Jan 2035 | $12,816.77 | $58.74 | $2,111.78 | $10,704.99 |
| Feb 2035 | $10,704.99 | $49.06 | $2,121.46 | $8,583.52 |
| Mar 2035 | $8,583.52 | $39.34 | $2,131.18 | $6,452.34 |
| Apr 2035 | $6,452.34 | $29.57 | $2,140.95 | $4,311.39 |
| May 2035 | $4,311.39 | $19.76 | $2,150.77 | $2,160.62 |
| Jun 2035 | $2,160.62 | $9.90 | $2,160.62 | $0.00 |
| End of year 10 | ||||
| Year | Opening balance | Interest | Principal | Ending balance |
|---|---|---|---|---|
| Year 1 | $200,000.00 | $10,614.85 | $15,431.45 | $184,568.55 |
| Year 2 | $184,568.55 | $9,744.40 | $16,301.91 | $168,266.64 |
| Year 3 | $168,266.64 | $8,824.84 | $17,221.47 | $151,045.17 |
| Year 4 | $151,045.17 | $7,853.42 | $18,192.89 | $132,852.28 |
| Year 5 | $132,852.28 | $6,827.19 | $19,219.11 | $113,633.17 |
| Year 6 | $113,633.17 | $5,743.08 | $20,303.22 | $93,329.95 |
| Year 7 | $93,329.95 | $4,597.82 | $21,448.48 | $71,881.46 |
| Year 8 | $71,881.46 | $3,387.96 | $22,658.35 | $49,223.12 |
| Year 9 | $49,223.12 | $2,109.85 | $23,936.46 | $25,286.66 |
| Year 10 | $25,286.66 | $759.65 | $25,286.66 | $0.00 |
What to Know About Amortization?
In accounting, amortization refers to the systematic expensing of an intangible asset’s cost (e.g., patents or goodwill) over its useful life. This reduces the asset’s book value on the balance sheet while recording periodic expenses on the income statement, reflecting its declining utility.
In finance, amortization is the process of paying off a debt, such as a mortgage, car loan, or personal loan, over time through a series of regular payments. These payments reduce the loan balance—a liability on the balance sheet—until it’s fully paid off. Amortization is available in the more specific calculators, like loan calculator or car loan calculator. Further here, we’ll cover especially financial amortization.
How Does Amortization Work?
To understand amortization fully, it’s helpful to explore how each payment is calculated and applied. This is best illustrated through an amortization schedule, a table that details every payment over the life of the loan.
Equal installment (A) for an amortized loan is determined using the annuity-immediate formula:
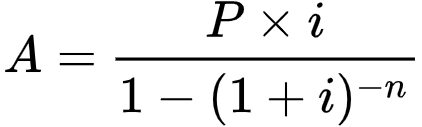
Where:
A = Total payment every period;
i = Periodic interest rate;
P = Present value, or the initial loan amount (principal);
n = Total number of installments.
Once the periodic payment (A) is known, the amortization schedule is built by calculating the interest and principal portions for each period:
- Interest Payment: Multiply the remaining loan balance by the monthly interest rate (i).
Example: If the balance is $200,000 and the monthly rate is 0.3333% (4% annual rate ÷ 12), the interest is $200,000 × 0.003333 = $666.67. - Principal Payment: Take away the interest payment from the total monthly payment (A).
Example: If A is $954.83, the principal payment is $954.83 - $666.67 = $288.16. - Remaining Balance: Take away the principal payment from the previous balance.
Example: $200,000 - $288.16 = $199,711.84.
This process repeats each period, with the interest payment decreasing (due to a lower balance) and the principal payment increasing, while the total payment stays constant.
Example Amortization Schedule
Consider a $200,000 mortgage with a 4% annual interest rate and a 30-year term (360 monthly payments). Using the annuity formula above, the monthly payment is approximately $954.83. Here’s how the first two payments might look:
| Date | Periodic Payment | Interest Payment | Principal Payment | Remaining Balance |
|---|---|---|---|---|
| 05/2024 | $954.83 | $666.67 | $288.16 | $199,711.84 |
| 06/2024 | $954.83 | $665.71 | $289.12 | $199,422.72 |
Over time, the interest portion shrinks, and the principal portion grows, accelerating the reduction of the balance until it reaches zero after 360 payments.
Hello, this is Publicalculator.com, your handy online resource where you'll find an array of calculators and problem-solving tools. We strive to simplify your daily calculations and provide you with fast and accurate answers.

